I got nerd sniped by Richard Stanley this week.
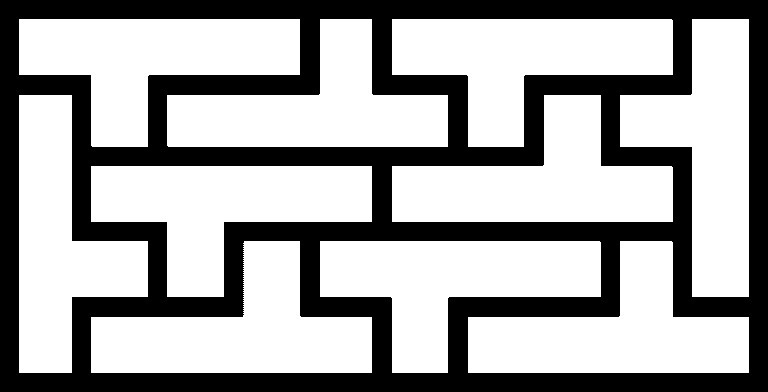
He https://mathoverflow.net/a/15306/104733 by suggesting that "people in the area believe" that it's undecidable whether or not a given polyomino, you can use it to tile a rectangle, as in the below picture.
He https://mathoverflow.net/a/15306/104733 by suggesting that "people in the area believe" that it's undecidable whether or not a given polyomino, you can use it to tile a rectangle, as in the below picture.
Comments
All of the 4-ominoes besides the S- (or Z-) shape are rectifiable, but you can prove that the S-shape can never tile a rectangle.
For example, check out this tiling of a 41×48 rectangle computed by https://github.com/eklhad/trec, which is the smallest rectangle that can be tiled by a particular 8-omino.
e.g. A126140(8) = 246, because in the last post we needed 246 copies of that 8-omino to tile a rectangle.
1, 1, 2, 4, 10, 92, 76, 246, 4
Here are some illustrations from https://cflmath.com/Polyomino/rectifiable_data.html illustrating a(5)=10, a(6)=92, and a(7)=76.
If, as many experts believe, it is Turing undecidable to determine whether or not a polyomino is rectifiable, then OEIS sequence A126140 https://mathoverflow.net/a/15306/104733! (!!!)
I took this picture just minutes before I went up to my hotel room to—coincidentally—teach my combinatorics students about https://en.wikipedia.org/wiki/Twelvefold_way.